Estimation of soil moisture from GPR data using Artificial Neural Networks

By / Research Papers / Leave a Comment / 27 December 2022
Post Views: 1,708

Abtract

Soil moisture estimation is essential for understanding the water cycle and its impact on weather and climate. GPR based soil moisture estimation is non-invasive in nature and provides quicker results as compared to standard laboratory approaches. Deep learning algorithms have been shown to be an effective method for extracting characteristics from GPR data. To assess soil moisture, this paper offers a deep artificial neural network (ANN) model. The data set was created using finite-difference-time-domain (FDTD) simulation and is used to train and validate the ANN model. The suggested model predicts soil moisture from GPR A-Scans well, with R2 = 0.998 and mean average percentage error (MAPE) of 1.23.

Authors

Nairit Barkataki*, Sharmistha Mazumdar*, Banty Tiru# and Utpal Sarma*

* Dept of Instrumentation & USIC, Gauhati University, Guwahati, India
# Dept of Physics, Gauhati University, Guwahati, India

Keywords. deep learning, regression, soil moisture, ground penetrating radar

Note:

This article was published in TRIBES 2021. You may cite the article using the following bibliographic data:

Nairit Barkataki, Sharmistha Mazumdar, Banty Tiru, Utpal Sarma: Estimation of soil moisture from GPR data using artificial neural networks. In: 2021 IEEE International Conference on Technology, Research, and Innovation for Betterment of Society (TRIBES), IEEE 2021, ISBN: 978-1-6654-3342-6.

© 2021 IEEE. Personal use of this material is permitted. Permission from IEEE must be obtained for all other uses, in any current or future media, including reprinting/republishing this material for advertising or promotional purposes, creating new collective works, for resale or redistribution to servers or lists, or reuse of any copyrighted component of this work in other works.

Contents
Contents
 1.  Introduction
 2.  GPR Data
 3.  Methodology
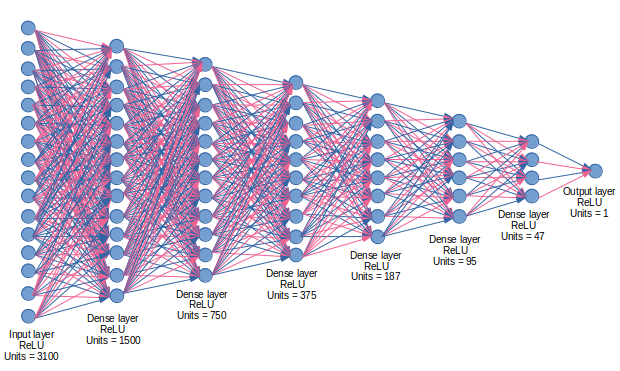
   3.1.  Proposed model
 4.  Results
 5.  Conclusion
 6.  Acknowledgement
1. Introduction

Soil moisture is considered to be a key variable in environmental studies such as meteorology, hydrology, agriculture and climate change. The estimation of soil moisture provides better understanding of the soil dynamics for making proactive decisions in the field of agriculture.

Soil moisture measurement is generally classified into direct and indirect techniques. Direct methods usually involve digging of holes to collect soil samples and then separating water from the collected samples. The separation of water from soil can be achieved by heating the soil samples or by chemical reactions [1]. These methods gives highly accurate results for a particular depth but they are expensive, time consuming and destructive [2].

Indirect methods mainly involve measurement of physical or chemical properties of soil that are dependent on the amount of soil moisture [1]. Previous studies shows that the electromagnetic (EM) properties of soil is correlated to its moisture content [3]. Time domain reflectrometry (TDR), ground penetrating radar (GPR) and some other techniques use EM properties for measurement of soil moisture.

Calamita et al. studied the variation in soil moisture with soil resistivity in the Vallaccia catchment (central Italy) using portable TDR, along with frequency domain reflectrometer sensors. The results were compared by applying various resistive methods and showed high correlation between resistivity and soil moisture [4]. However, TDR probes limits the depth of investigation to a few meters [5].

Brocca et al. explored the reliability soil moisture estimation from satellite data. Correlation values of relative soil moisture increase upto 0.81 upon application of different filters but decrease with increase in vegetation [6].

Salam et al. developed a real time, in-situ method based on wireless underground communications (WUC) for estimation of soil permittivity and moisture. To obtain highly accurate results, studies were carried out in the frequency range of 100–500 MHz with the antenna buried at 10 cm-40 cm depths in various soils [7].

Compared to TDR, GPR technique has the advantage of giving data from greater spatial regions. GPR has been widely used in sedimentary research [8] and for estimating water content of soil [9][10][11].

GPR is widely used for object size detection [12][13]. However, the size of a target observable with a GPR is dependent on the antenna’s centre frequency [14]. The frequency useful for different applications depends on the soil properties such as soil moisture [2] and soil type [15]. Thus, prior knowledge about the soil moisture content of the soil helps in determining the appropriate frequency to be used for a particular application.

Hubbard et al. examined the potential of estimating soil moisture over large areas with varying hydrological conditions using GPR reflections [16]. Benedetto et al. proposed an approach to estimate soil moisture for pavement inspection using GPR. The results were validated using capacitance probes [17].

However, the interpretation of GPR data is still a manual process. It is done by people who have extensive experience in GPR data interpretation. Of late, machine learning algorithms have been implemented for processing and interpretation of GPR data. Rahman et al. predicted 11 soil series using machine learning techniques in order to find appropriate crops for cultivation [18]. Senanayake et al. developed an neural network model to estimate catchment scale soil moisture fom remote sensing and GPR data [19]. A long short-term memory (LSTM) predictive framework integrated with Boruta-random forest (BRF) optimiser was proposed by Ahmed et al. to estimate soil moisture under global warming scenarios [20]. An SVM model was proposed by Malajner et al. to classify soil types [21]. After determining the soil type, another model for estimating soil moisture was employed. Ultra-wideband radio frequency modules and antennas were used to capture the data. Recently, various regression and machine learning models were proposed by Teneja et al. to predict soil organic matter and soil moisture content using images taken from cell phones [22].

Although various remote sensing techniques are utilised to estimate soil moisture, further research is needed to investigate the feasibility of assessing soil moisture content using GPR. This paper mainly focuses on

  1. Creation of a synthetic GPR database for estimation of soil moisture.
  2. Development of a regression model to estimate soil moisture with a high degree of accuracy.
2. GPR Data GprMax, an open source electromagnetic simulator, is used to generate the database. It uses FDTD method for simulation of GPR model. Each simulated model has dimensions of $1000~mm\times400~mm\times600~mm$ ($X\times Y\times Z$). The top 200 mm of the model’s overall height, i.e. 600 mm, is an air layer, while the remaining 400 mm is a soil layer. Soil moisture is varied randomly between 1\% and 10\% and the corresponding values of relative permittivity ($\varepsilon_r$) and conductivity ($\sigma$) are used in simulation. Table I shows the soil permittivity and conductivity as a function of moisture content [23]. For fractional values of soil moisture, the corresponding values of $\varepsilon_r$ and $\sigma$ are interpolated.
TABLE I: Relative permittivity and conductivity corresponding to moisture content in soil
S. No.Soil Moisture
Relative
Permitivity
εr
Conductivity
σ(S/m)
×10–⁢6
11%3.23439.9
22%3.468618.8
33%3.702927.7
44%3.937236.6
56%4.405854.5
67%4.640163.4
78%4.874472.3
89%5.108781.2
910%5.34390.1
A cylindrical object of aluminium ($\varepsilon_r$ = 10.8 and $\sigma$ = $3.5\times10^7$ S/m) is placed underneath the soil surface. The object depth varies from 25 mm to 365 mm from the top of the soil layer and the object radius has values between 9 mm to 20 mm. The depth and radius values are chosen randomly using a program. A simulated model with a cylindrical object buried in the soil is shown in Figure 1.
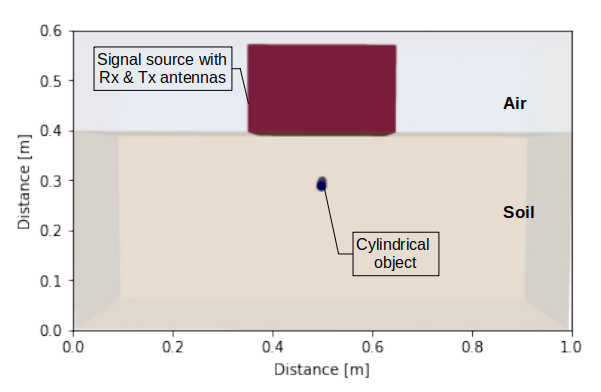
P006_Simulated_model1.png
Figure1. Simulated model
The simulation time window must be long enough for the EM waves to travel through the medium to the cylindrical object and then reflect back to the receiver. However, the time window depends on the relative permittivity of the soil. In this case, the value of time window is taken such that it is suitable for all the different values of soil moisture. The different parameters used while simulating the GPR models are given in Table II. A simulated A-Scan having 6\% of moisture in soil is shown in Figure 2.
TABLE II: Simulation parameters
Sl. No.Simulation
Parameter		Values
1Excitation waveformGaussian
2Frequency used400 MHz
3Spatial resolution2 mm
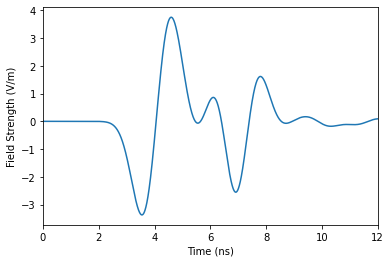
4Time window12 ns
P006_A-Scan1.png
Figure2. Simulated A-Scan
A total of 2690 A-Scans are generated, each having 3113 data points along the depth of the model. The dataset contains around 8 million data points. NVIDIA GPU RTX3090 is used to accelerate the simulation and generate the dataset. 85\% of the dataset is used to train and validate the model and 15\% of it is kept for testing the model. The dataset is normalised before training the model.
P006_ANN_architecture1.png
Figure3. Proposed ANN architecture
3. Methodology In this work, an ANN model is used. An ANN model consists of multiple layers, each of which has one or more neurons or units. Each of these neurons is linked to every other neuron in the following layer. In ANN, feature extraction is performed hierarchically, with increments after each layer. Forward propagation and back propagation are the two stages of ANN. Forward propagation entails assigning weights and biases to each neuron in a layer, as well as applying an activation function to each neuron. A loss function is used to calculate the error between the true and predicted values. Using an optimisation function, backward propagation assists in determining optimal parameter values for the model, by minimising the loss function. 3.1. Proposed model Initially, 3113 neurons were used in the input layer. Multiple hidden layers were added after the input layer which had half the number of neurons than the previous layers. After tuning the number of neurons through multiple training runs, the optimised model is found to have 3100 units in the input layer, followed by 6 hidden layers having 1500, 750, 375, 187, 95 and 47 units respectively, as shown in Figure 3. The output layer contains a single unit that produces the predicted values. All the layers in the neural network implement the function: \begin{equation} output = activation(dot(input, kernel) + bias) \end{equation} where “activation” is the activation function for the layer, “kernel” is the weights matrix created by the layer, “bias” is the bias vector created by the layer. Each layer’s activation function is a Rectified Linear Unit (ReLU), which can be described mathematically as shown in eq2 \begin{equation} \label{eq2} f(x) = max(0,x) \end{equation} where x is a neuron’s input. If x is less than zero, the activation function f(x) returns 0; otherwise, it returns x (input). To train a deep learning model, the input data is fed to the model and predictions are generated. The predicted values are compared to the actual values and the loss is calculated using a loss function. The loss function used in this study is Mean Absolute Percentage Error (MAPE). Adaptive gradient (AdaGrad) algorithm is used to optimise the model with an initial learning of $1\times10^{-5}$. The training and validation losses over 300 epochs is shown in Figure 4. The GPR data processing pipeline is written in python along with Keras and Tensorflow frameworks for application of deep learning algorithms.
P006_MAPE_plot1.png
Figure4. Loss curve during training and validation of the model
4. Results
TABLE III: Predicted values of soil moisture by the ANN model
Sl. No.True
Value (%)		Best Predicted
Value (%)		Worst Predicted
Value (%)		Median of
Predicted Values (%)
110.9991.4670.999
222.0021.9081.992
332.9993.4513.008
443.9994.2444.005
566.0006.3426.008
677.0017.3557.009
788.0017.7378.014
898.9999.5369.033
91010.0009.4889.927
429 A-Scans are used for final performance evaluation of the proposed model. The best and worst predicted values corresponding the different values of soil moisture are given in Table III. Moreover, different metrics such as mean squared error (MSE), mean absolute error (MAE), mean squared logarithmic error (MSLE), mean absolute percentage error (MAPE) and R-squared are used to analyse the performance of the ANN model as given in Table IV.
TABLE IV: Performance metrics of the ANN model
MetricsPerformance of the ANN model
MSE9.562×10–7
MAE0.00055
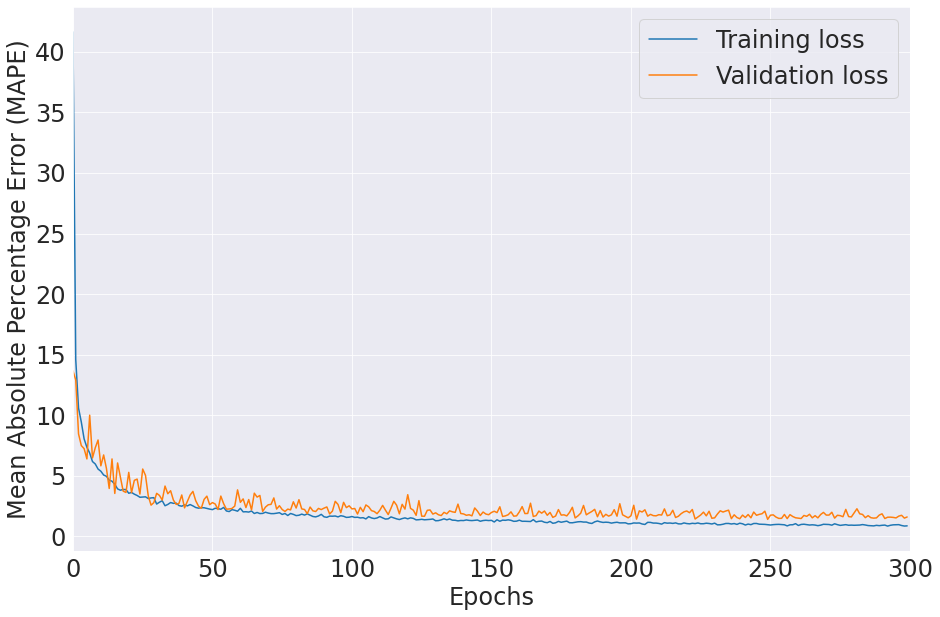
MAPE1.232291
MSLE8.344×10–7
R-squared0.998
5. Conclusion This study presented a ANN model for estimating soil moisture from GPR A-Scan data. The overall performance of the model was evaluated using the metrics listed in Table IV. The most popular statistical metric for a regression problem is R-squared whose value lies between 0 and 1. In order for a regression model to be reliable, the value should be greater than 0.95. The proposed model achieves an R-squared value of 0.998 and MAPE of 1.23 on the test set, demonstrating its high reliability. A comparison with previously reported literature work is shown in Table V. Most of the techniques used to estimate soil moisture are invasive in nature. Moreover, soil moisture estimation was done using satellite data and laboratory-based methods, which rarely produced results in real time. The proposed work uses GPR, non-invasive method, to collect data. This will lead to faster data collection and is capable of producing results in real time.
TABLE V: Comparison of present work with past studies
Sl. No.AuthorsTechnique usedReal time/
Offline		𝐑𝟐
1Lee et al.
(2018) [24]		Deep neural network applied on remotely sensed satellite data (non-invasive)Offline0.79
2Koley et al.
(2020) [25]		Surface soil moisture estimated using LST-NDVI feature space from satellite data (non-invasive)Offline0.8
3Taneja et al.
(2021) [22]		Machine learning algorithms applied on soil sample images collected using cell phone. (invasive)Offline0.95
4Present workANN applied on GPR data (non-invasive)Real time0.998
However, the proposed model is trained and tested in dataset with limited variation of soil moisture. In real scenarios, different environmental factors might lead to large variations in soil moisture. To improve the proposed model, the authors plan to implement the proposed model on real data. 6. Acknowledgement The authors are grateful to Google for providing Google Colaboratory, a computational platform, used for training and evaluation of the proposed model.

References

  1. Martin R Carter and Edward Gerard Gregorich (2007): Soil sampling and methods of analysis. CRC press, 2007.
  2. Xiuwei Liu and Xuejun Dong and Daniel I Leskovar (2016): Ground penetrating radar for underground sensing in agriculture: a review. In: International Agrophysics, vol. 30, no. 4, 2016.
  3. Roberta Porretta and Fabio Bianchi (2016): Profiles of relative permittivity and electrical conductivity from unsaturated soil water content models. In: Annals of Geophysics, vol. 59, no. 3, pp. 0320, 2016.
  4. G Calamita and L Brocca and A Perrone and S Piscitelli and V Lapenna and F Melone and T Moramarco (2012): Electrical resistivity and TDR methods for soil moisture estimation in central Italy test-sites. In: Journal of Hydrology, vol. 454, pp. 101–112, 2012.
  5. G Clarke Topp and GW Parkin and Ty PA Ferré and MR Carter and EG Gregorich (2008): Soil water content. In: Soil sampling and methods of analysis, pp. 939–962, 2008.
  6. Luca Brocca and Stefan Hasenauer and T Lacava and F Melone and T Moramarco and W Wagner and W Dorigo and P Matgen and J Mart'inez-Fernández and P Llorens and others (2011): Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. In: Remote Sensing of Environment, vol. 115, no. 12, pp. 3390–3408, 2011.
  7. Abdul Salam and Mehmet C Vuran and Suat Irmak (2019): Di-Sense: In situ real-time permittivity estimation and soil moisture sensing using wireless underground communications. In: Computer Networks, vol. 151, pp. 31–41, 2019.
  8. Adrian Neal (2004): Ground-penetrating radar and its use in sedimentology: principles, problems and progress. In: Earth-science reviews, vol. 66, no. 3-4, pp. 261–330, 2004.
  9. Johan Alexander Huisman and Susan Sharpess Hubbard and J David Redman and A Peter Annan (2003): Measuring soil water content with ground penetrating radar: A review. In: Vadose zone journal, vol. 2, no. 4, pp. 476–491, 2003.
  10. Anja Klotzsche and François Jonard and Majken Caroline Looms and Jan Kruk and Johan A Huisman (2018): Measuring soil water content with ground penetrating radar: A decade of progress. In: Vadose Zone Journal, vol. 17, no. 1, pp. 1–9, 2018.
  11. MH Zhang and M Bano and X Feng and N Lesparre and JF Girard and O Razakarisoa and B Belfort and F Lehmann and P Friedmann (2021): Estimating water content of unsaturated sandy soils by GPR during a drainage experiment. In: IOP Conference Series: Earth and Environmental Science, pp. 012018, IOP Publishing 2021.
  12. Nairit Barkataki and Sharmistha Mazumdar and Rajdeep Talukdar and Priyanka Chakraborty and Banty Tiru and Utpal Sarma (2020): Prediction of Size of Buried Objects using Ground Penetrating Radar and Machine Learning Techniques. In: 2020 International Conference on Computational Performance Evaluation (ComPE), pp. 781-785, IEEE 2020.
  13. Iraklis Giannakis and Antonios Giannopoulos and Craig Warren (2020): A machine learning scheme for estimating the diameter of reinforcing bars using ground penetrating radar. In: IEEE Geoscience and Remote Sensing Letters, 2020.
  14. Nairit Barkataki and Banty Tiru and Utpal Sarma (2021): Performance investigation of patch and bow-tie antennas for ground penetrating radar applications. In: International Journal of Advanced Technology and Engineering Exploration, vol. 8, no. 79, pp. 753–765, 2021, ISSN: 2394-7454.
  15. Nairit Barkataki and Sharmistha Mazumdar and P Bipasha Devi Singha and Jyoti Kumari and Banty Tiru and Utpal Sarma (2021): Classification of soil types from GPR B Scans using deep learning techniques. In: 2021 6th IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT 2021), pp. 840–844, IEEE 2021.
  16. IA Lunt and SS Hubbard and Y Rubin (2005): Soil moisture content estimation using ground-penetrating radar reflection data. In: Journal of hydrology, vol. 307, no. 1-4, pp. 254–269, 2005.
  17. Andrea Benedetto and Fabio Tosti and Bianca Ortuani and Mauro Giudici and Mauro Mele (2013): Soil moisture mapping using GPR for pavement applications. In: 2013 7th International Workshop on Advanced Ground Penetrating Radar, pp. 1–5, IEEE 2013.
  18. Sk Al Zaminur Rahman and Kaushik Chandra Mitra and SM Mohidul Islam (2018): Soil classification using machine learning methods and crop suggestion based on soil series. In: 2018 21st International Conference of Computer and Information Technology (ICCIT), pp. 1–4, IEEE 2018.
  19. IP Senanayake and I-Y Yeo and JP Walker and GR Willgoose (2021): Estimating catchment scale soil moisture at a high spatial resolution: Integrating remote sensing and machine learning. In: Science of The Total Environment, vol. 776, pp. 145924, 2021.
  20. AA Masrur Ahmed and Ravinesh C Deo and Afshin Ghahramani and Nawin Raj and Qi Feng and Zhenliang Yin and Linshan Yang (2021): LSTM integrated with Boruta-random forest optimiser for soil moisture estimation under RCP4. 5 and RCP8. 5 global warming scenarios. In: Stochastic Environmental Research and Risk Assessment, pp. 1–31, 2021.
  21. Marko Malajner and Dusan Gleich and Peter Planinsic (2019): Soil type characterization for moisture estimation using machine learning and UWB-Time of Flight measurements. In: Measurement, vol. 146, pp. 537–543, 2019.
  22. Perry Taneja and Hitesh Kumar Vasava and Prasad Daggupati and Asim Biswas (2021): Multi-algorithm comparison to predict soil organic matter and soil moisture content from cell phone images. In: Geoderma, vol. 385, pp. 114863, 2021.
  23. J Padarian and B Minasny and AB McBratney (2019): Using deep learning to predict soil properties from regional spectral data. In: Geoderma Regional, vol. 16, pp. e00198, 2019.
  24. Chang Suk Lee and Eunha Sohn and Jun Dong Park and Jae-Dong Jang (2018): Estimation of soil moisture using deep learning based on satellite data: A case study of South Korea. In: GIScience & Remote Sensing, vol. 56, no. 1, pp. 43–67, 2018.
  25. Swadhina Koley and C. Jeganathan (2020): Estimation and evaluation of high spatial resolution surface soil moisture using multi-sensor multi-resolution approach. In: Geoderma, vol. 378, pp. 114618, 2020, ISSN: 0016-7061.

Related Posts

Leave a Comment

Your email address will not be published. Required fields are marked *